Partition
- Kth Largest Element in an Array
1. Kth Largest Element in an Array
quick sort 的变形
唔，需要好好理解下这道quick sort的变形题。
有好几种解法，根据性能优化来讲。
- Arrays.sort + 直接用index来access value: O(N log N) + O(1) memory
- Priority Queue with size of K + iterate through the list: O(N log K) + O(k)
- quick sort: O(N) best case / O(N^2) worst case running time + O(1) memory
- randomized quick sort
重点理解下quick sort + randomized quick sort
2. Kth Smallest Element in a Sorted Matrix
3. Sort Colors
three way partition
需要好好理解下几个Pointer是怎么移动的。
demo可以参考Princeton课件里的dijkstra's 3 way partition
算法公式是
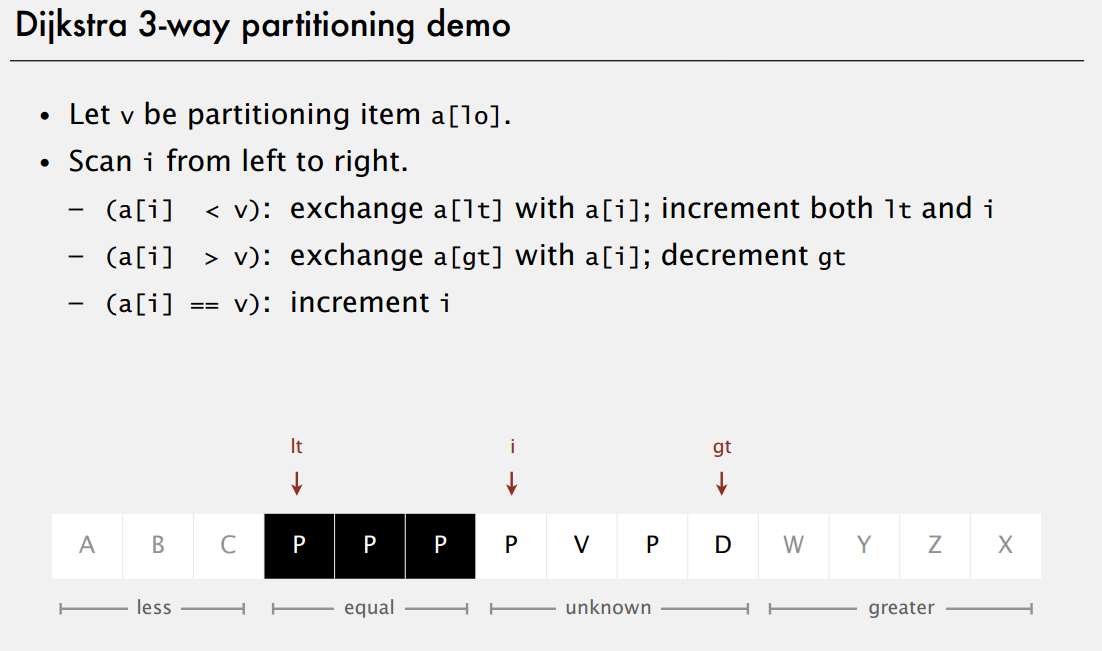终止条件 i <= right；跟right交换的时候，不需要i ++，其他两种情况都要i ++，因为gt指针是未知元素，需要再判断。
[0, left - 1] 是 < v的元素，[left, i - 1] 是 = v的元素，[i, right] 是未知元素。
4. Sort Colors II
- counting sort: O(n) time, O(k) space
- sort on each individual colors: O(n^2) time, O(1)
- quick sort: O(n log n) time
- customized quick sort: O(n log k) time
- Counting Sort: 因为已经知道了range是[1, k]， 所以可以建个k长的array, 数每个元素有多少个，然后再填回去。
public class Solution {
/**
* Method I: O(k) space, O(n) time; two-pass algorithm, counting sort
* @param colors: A list of integer
* @param k: An integer
* @return: nothing
*/
public void sortColors2TwoPass(int[] colors, int k) {
int[] count = new int[k];
for (int color : colors) {
count[color-1]++;
}
int index = 0;
int colorNum = 1;
for (int occur: count) {
while (occur > 0) {
colors[index] = colorNum;
index++;
occur--;
}
colorNum++;
}
}
}
Sort on each individual color:
- 用两个pointers，初始位置为0和length - 1，因为已经知道了range为[1, k]，那么每次可以把数字和min & max数字比较，如果在== min || max 之外的话，则swap。
- each time sort the array into 3 parts: [sorted min array], [unsorted], [sorted max array]
[0, left - 1] ，[left, i - 1] ，[i, right]
O(n^ 2) = T(n - 2) + n
public class Solution {
public void sortColorsII(int[] colors, int k) {
if (colors == null || colors.length <= 1) return;
int left = 0, right = colors.length - 1;
int min = 1, max = k;
int currt = 0;
while (min < max) {
//template
while (currt <= right) {
if (colors[currt] == min) {
swap(colors, currt, left);
currt++;
left++;
} else if (colors[currt] == max) {
swap(colors, currt, right);
right--;
} else { // within in the range
currt++;
}
}
//unsorted subarray starts from the left pointer
currt = left;
min++;
max--;
}
}
}
- Normal Quick Sort
public void sortKColors1(int[] colors, int k) {
10 // write your code here
11 if (colors == null) {
12 return;
13 }
14
15 quickSort(colors, 0, colors.length - 1);
16 }
17
18 public void quickSort(int[] colors, int left, int right) {
19 if (left >= right) {
20 return;
21 }
22
23 int pivot = colors[right];
24
25 int pos = partition(colors, left, right, pivot);
26
27 quickSort(colors, left, pos - 1);
28 quickSort(colors, pos + 1, right);
29 }
30
31 public int partition(int[] colors, int left, int right, int pivot) {
32 int leftPoint = left - 1;
33 int rightPoint = right;
34
35 while (true) {
36 while (colors[++leftPoint] < pivot);
37
38 while (leftPoint < rightPoint && colors[--rightPoint] > pivot);
39
40 if (leftPoint >= rightPoint) {
41 break;
42 }
43
44 swap(colors, leftPoint, rightPoint);
45 }
46
47 swap(colors, leftPoint, right);
48 return leftPoint;
49 }
50
51 public void swap(int[] colors, int left, int right) {
52 int tmp = colors[left];
53 colors[left] = colors[right];
54 colors[right] = tmp;
55 }
- Customized Quick Sort
// version 1: O(nlogk), the best algorithm based on comparing
class Solution {
/**
* @param colors: A list of integer
* @param k: An integer
* @return: nothing
*/
public void sortColors2(int[] colors, int k) {
if (colors == null || colors.length == 0) {
return;
}
rainbowSort(colors, 0, colors.length - 1, 1, k);
// sortColorsII(colors, k);
}
public void rainbowSort(int[] colors,
int left,
int right,
int colorFrom,
int colorTo) {
if (colorFrom == colorTo) {
return;
}
if (left >= right) {
return;
}
int colorMid = (colorFrom + colorTo) / 2;
int l = left, r = right;
while (l <= r) {
while (l <= r && colors[l] <= colorMid) {
l++;
}
while (l <= r && colors[r] > colorMid) {
r--;
}
if (l <= r) {
int temp = colors[l];
colors[l] = colors[r];
colors[r] = temp;
l++;
r--;
}
}
rainbowSort(colors, left, r, colorFrom, colorMid);
rainbowSort(colors, l, right, colorMid + 1, colorTo);
}
}