Array
rotated array,利用A[mid] and A[end]的关系,来进行接下来的判断
3. Find Minimum in Rotated Sorted Array
A[mid] > A[right] 时,mid 在左半边,最小值一定在 mid 右侧;
A[mid] <= A[right] 时,mid 在右半边,最小值一定在 mid 左侧;
4. Search in Rotated Sorted Array
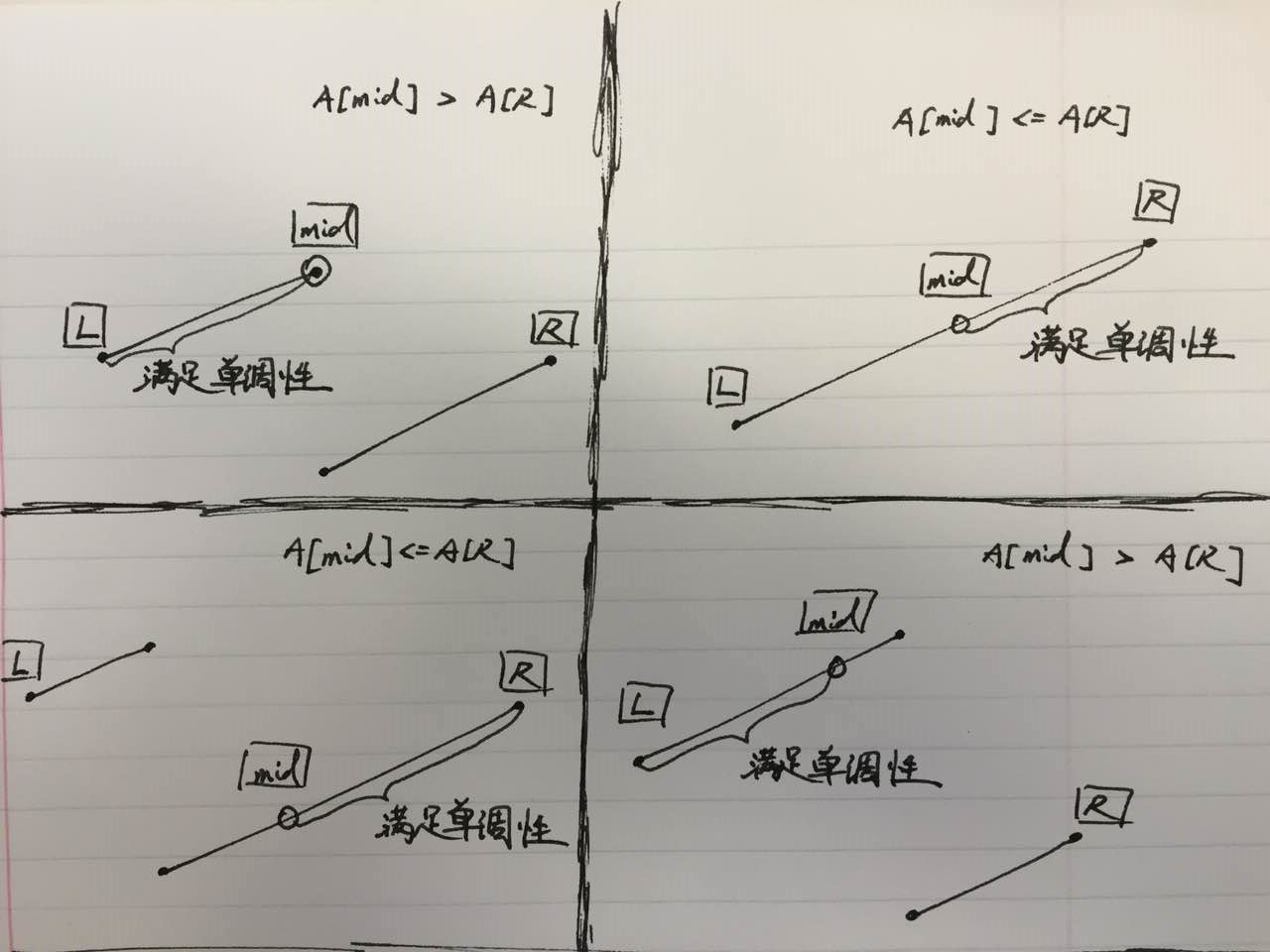
根据mid point和right pointer的关系,来判断单调性。
可以根据 A[mid] 与 A[right] 的大小关系,先行判断 mid 一定位于哪一端;
对于已经确定 mid 左/右 的数组,必然有一段区间满足单调性,可以利用来做 binary search.
注意:边界可相等=
class Solution {
public int search(int[] nums, int target) {
if (nums == null || nums.length == 0) return -1;
int start = 0, end = nums.length - 1;
while (start + 1 < end) {
int mid = start + (end - start) / 2;
if (nums[mid] <= nums[end]) {
if (nums[mid] <= target && target <= nums[end]) {
start = mid;
} else {
end = mid;
}
} else {
if (nums[start] <= target && target <= nums[mid]) {
end = mid;
} else {
start = mid;
}
}
}
if (nums[start] == target) return start;
else if (nums[end] == target) return end;
return -1;
}
}
5. Find Minimum in Rotated Sorted Array II
A[mid] > A[right] 时,mid 在左半边,最小值一定在 mid 右侧;
A[mid] <= A[right] 时,mid 在右半边,最小值一定在 mid 左侧;
A[mid] == A[right] 时,无法判断,把 right 向左挪一格。
跟I很像,唯一的区别就是这道题有了duplicateds,因此在对待nums[mid] == nums[right]的时候,就需要不同的操作了。
public boolean search(int[] nums, int target) {
if (nums == null || nums.length == 0) return false;
int start = 0, end = nums.length - 1;
while (start + 1 < end) {
int mid = start + (end - start) / 2;
if (nums[mid] == target) return true;
if (nums[mid] < nums[end]) {
if (nums[mid] <= target && target <= nums[end]) {
start = mid;
} else {
end = mid;
}
} else if (nums[mid] > nums[end]){//mid > right: on two diff lines
if (nums[start] <= target && target <= nums[mid]) {
end = mid;
} else {
start = mid;
}
} else {
end--;
}
}
return nums[start] == target || nums[end] == target;
}
6. Single Element in a Sorted Array
- find the left num of the middle pair
关键在于log(n)的time complexity,提示了可能用binary search来做。
这题有好几种做法。
- 小伙伴,成对找。
- 找到中间的一对小伙伴中的左边的那个,也就是Mid必须得是偶数。
如果Mid 和Mid后面的那个小伙伴是一对的话,那么说明这对小伙伴的左边的伙伴们都是成双成对的。单身狗在右半边。
如果Mid和Mid后面的那个小伙伴不是一对的话,那么说明这位置对不上,左边的伙伴们肯定有一个单身狗。
class Solution {
public int singleNonDuplicate(int[] nums) {
if (nums == null || nums.length == 0) return -1;
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (mid % 2 == 1) mid--;
// We found a pair. The single element must be on the right.
// Example: |1 1 3 3 5 6 6|
// ^ ^
// Next: 1 1 3 3|5 6 6|
if (nums[mid] == nums[mid + 1]) {
left = mid + 2;
} else {
// We didn't find a pair. The single element must be on the left.
// (pipes mean start & end)
// Example: |0 1 1 3 3 6 6|
// ^ ^
// Next: |0 1 1|3 3 6 6
right = mid;
}
}
return nums[left];
}
}
还有其他的方法,可以参考